上一节介绍了最简单的交换排序 - 冒泡排序，这一节将介绍平均性能比冒泡排序要好很多的一种交换排序，那就是快排序(Quick Sort)。

快排序的基本思想

快排序(Quick Sort)是一种分治的排序算法。

• 首先从待排序对象中选出一个基准对象(Pivot)， 通常取第一个对象;
• 然后调整所有待排序对象，将基准对象放置到某个特定的位置，使基准对象左边的所有对象的关键字都小于等于基准对象的关键字，使基准对象右边的所有对象的关键字都大于等于基准对象的关键字；
• 最后把基准对象左边的那些对象与基准对象右边的那些对象分别看做两个独立的序列，再对这两个序列分别(递归调用快排序算法)排序。

典型的快排序过程是这样子滴，图片来源戳。

快速排序之所以比较快，是因为相对于冒泡排序来说，每次交换都是跳跃式的。每次排序的时候设置一个基准对象(Pivot)，将关键字小于等于基准对象的关键字的所有对象都放置到基准对象的左边，将关键字大于等于基准对象的关键字的所有对象都放置到基准对象的右边。这样在每次交换的时候就不会像冒泡排序一样只能在相邻的对象之间进行交换，交换的距离就大得多了。因此，总的比较和交换次数就减少了，速度自然也就提高了。

o 快排序(Quick Sort)的C代码实现

1 /* 2  * Basic Idea of QuickSort 3  * 4  * 1. Pick an element in the array as the pivot element 5  * 6  * 2. Make a pass to the array, called the PARTITION step, which rearranges 7  *    the elements in the array: 8  *    a. The pivot element is in the proper place 9  *    b. The elements less    than pivot element are on the left  of it10  *    c. The elements greater than pivot element are on the right of it11  *12  * 3. Recursively apply the above process to the left and right part of13  *    the pivot element14  */15 16 #define QSORT(a, n)     quicksort(a, 0, n - 1)17 18 void quicksort(int a[], int left, int right)19 {20         if (right <= left)21                 return;22 23         int j = partition(a, left, right); // PARTITION24         quicksort(a, left,  j - 1); // sort left  part a[left .. j-1]25         quicksort(a, j + 1, right); // sort right part a[j+1  .. right]26 }27 28 static int partition(int a[], int left, int right)29 {30         // left and right scan indices31         int i = left + 1;32         int j = right;33 34         // get partitioning item i.e. pivot35         int pivot = a[left];36 37         // scan right, scan left, check for scan complete, and exchange38         while (1) {39                 for (; j > left; j--) { // scan right40                         if (a[j] < pivot)41                                 break;42                 }43 44                 for (; i < right; i++) { // scan left (i<=right also works but unnecessary)45                         if (a[i] > pivot)46                                 break;47                 }48 49                 if (i >= j)50                         break;51 52                 exchange(a, i, j);53         }54 55         //56         // put pivot = a[j] into the right position, with57         //      a[left .. j-1] <= a[j] <= a[j+1 .. right]58         //59         exchange(a, left, j);60 61         return j;62 }63 64 static void exchange(int a[], int i, int j)65 {66         int t = a[i];67         a[i] = a[j];68         a[j] = t;69 }

接下来，给出一个完整的qsort.c并编译后测试, 以便形象化地理解冒泡排序的全过程。

o qsort.c 注意：下面的程序中某些代码行风格很不好是故意的，因为只是为了帮助打印排序过程故一切从简。

1 #include 
     
        2 #include 
      
         3   4 typedef struct obs_s {  5         unsigned int loop;  6         unsigned int swap;  7 } obs_t;  8   9 obs_t g_obs = { .loop = 0, .swap = 0 }; 10  11 size_t n = 0; /* size of array */ 12  13 static void show(int a[], size_t n); 14 static void exchange(int a[], int i, int j); 15 static int partition(int a[], int left, int right); 16  17 #define QSORT(a, n)     quicksort(a, 0, n - 1) 18  19 void quicksort(int a[], int left, int right) 20 { 21         if (right <= left) 22                 return; 23  24         int j = partition(a, left, right); // PARTITION 25         quicksort(a, left,  j - 1); // sort left  part a[left .. j-1] 26         quicksort(a, j + 1, right); // sort right part a[j+1  .. right] 27 } 28  29 static int partition(int a[], int left, int right) 30 { 31         // left and right scan indices 32         int i = left + 1; 33         int j = right; 34  35         // get partitioning item i.e. pivot 36         int pivot = a[left]; 37  38         // scan right, scan left, check for scan complete, and exchange 39         while (1) { 40                 for (; j > left; j--) { g_obs.loop++; // scan right 41                         if (a[j] < pivot) 42                                 break; 43                 } 44  45                 for (; i < right; i++) { g_obs.loop++; // scan left 46                         if (a[i] > pivot) 47                                 break; 48                 } 49  50                 if (i >= j) 51                         break; 52  53                 g_obs.swap++; 54                 printf("#%d:%d\t\t", left, right); show(a, n); 55                 printf("\t<-- swap(a[%d], a[%d])\n", i, j); 56  57                 exchange(a, i, j); 58         } 59  60         // 61         // put pivot = a[j] into the right position, with 62         //      a[left .. j-1] <= a[j] <= a[j+1 .. right] 63         // 64         g_obs.swap++; 65         printf("#%d:%d\t\t", left, right); show(a, n); 66         printf("\t<-- swap(a[%d], a[%d])\t next pivot : a[%d]\n", left, j, j); 67  68         exchange(a, left, j); 69  70         return j; 71 } 72  73 static void exchange(int a[], int i, int j) 74 { 75         int t = a[i]; 76         a[i] = a[j]; 77         a[j] = t; 78 } 79  80 static void show(int a[], size_t n) 81 { 82         for (int i = 0; i < n; i++) 83                 printf("%c  ", a[i]); 84 } 85  86 int main(int argc, char *argv[]) 87 { 88         if (argc < 2) { 89                 fprintf(stderr, "Usage: %s 
       
         [C2] ...\n", argv[0]); 90                 return -1; 91         } 92  93         argc--; 94         argv++; 95  96         n = argc; 97         int *a = (int *)malloc(sizeof(int) * n); 98 #define VALIDATE(p) do { if (p == NULL) return -1; } while (0) 99         VALIDATE(a);100 101         for (int i = 0; i < n; i++)102                 *(a+i) = argv[i][0];103 104         printf("                ");105         for (int i = 0; i < n; i++)106                 printf("%-2d ", i);107         printf("\n");108 109         printf("Before sorting: "); show(a, n); printf("\n");110         QSORT(a, n);111         printf("After  sorting: "); show(a, n); printf("\n");112 113         printf("\n");114         printf("Total loop times : %2d\n", g_obs.loop);115         printf("Total swap times : %2d\n", g_obs.swap);116 117         free(a); a = NULL;118         return 0;119 }
       
      
     

o 编译并测试

$  gcc -g -Wall -m32 -std=c99 -o qsort qsort.c$ ./qsort       K  R  A  T  E  L  E  P  U  I  M  Q  C  X  O  S                0  1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 Before sorting: K  R  A  T  E  L  E  P  U  I  M  Q  C  X  O  S  #0:15           K  R  A  T  E  L  E  P  U  I  M  Q  C  X  O  S  <-- swap(a[1], a[12])#0:15           K  C  A  T  E  L  E  P  U  I  M  Q  R  X  O  S  <-- swap(a[3], a[9])#0:15           K  C  A  I  E  L  E  P  U  T  M  Q  R  X  O  S  <-- swap(a[5], a[6])#0:15           K  C  A  I  E  E  L  P  U  T  M  Q  R  X  O  S  <-- swap(a[0], a[5])   next pivot : a[5]#0:4            E  C  A  I  E  K  L  P  U  T  M  Q  R  X  O  S  <-- swap(a[0], a[2])   next pivot : a[2]#0:1            A  C  E  I  E  K  L  P  U  T  M  Q  R  X  O  S  <-- swap(a[0], a[0])   next pivot : a[0]#3:4            A  C  E  I  E  K  L  P  U  T  M  Q  R  X  O  S  <-- swap(a[3], a[4])   next pivot : a[4]#6:15           A  C  E  E  I  K  L  P  U  T  M  Q  R  X  O  S  <-- swap(a[6], a[6])   next pivot : a[6]#7:15           A  C  E  E  I  K  L  P  U  T  M  Q  R  X  O  S  <-- swap(a[8], a[14])#7:15           A  C  E  E  I  K  L  P  O  T  M  Q  R  X  U  S  <-- swap(a[9], a[10])#7:15           A  C  E  E  I  K  L  P  O  M  T  Q  R  X  U  S  <-- swap(a[7], a[9])   next pivot : a[9]#7:8            A  C  E  E  I  K  L  M  O  P  T  Q  R  X  U  S  <-- swap(a[7], a[7])   next pivot : a[7]#10:15          A  C  E  E  I  K  L  M  O  P  T  Q  R  X  U  S  <-- swap(a[13], a[15])#10:15          A  C  E  E  I  K  L  M  O  P  T  Q  R  S  U  X  <-- swap(a[10], a[13]) next pivot : a[13]#10:12          A  C  E  E  I  K  L  M  O  P  S  Q  R  T  U  X  <-- swap(a[10], a[12]) next pivot : a[12]#10:11          A  C  E  E  I  K  L  M  O  P  R  Q  S  T  U  X  <-- swap(a[10], a[11]) next pivot : a[11]#14:15          A  C  E  E  I  K  L  M  O  P  Q  R  S  T  U  X  <-- swap(a[14], a[14]) next pivot : a[14]After  sorting: A  C  E  E  I  K  L  M  O  P  Q  R  S  T  U  X  Total loop times : 69Total swap times : 17

以上排序过程截图如下(截图来源: Algorithms Fourth Edition P289)

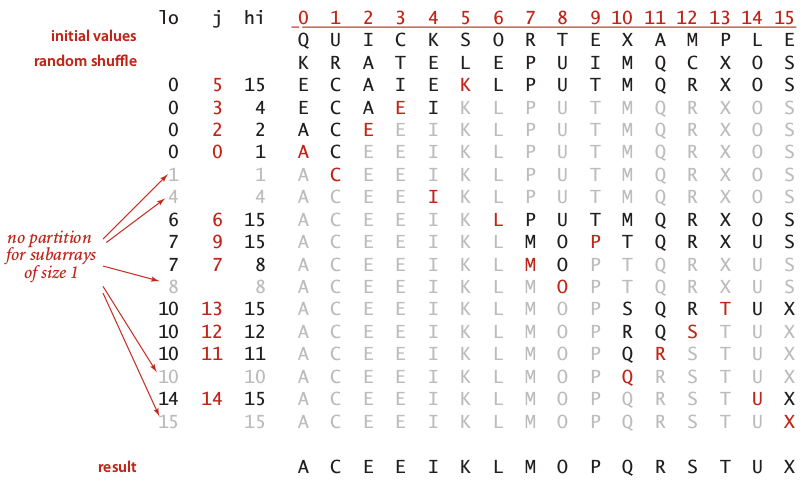
小结： 快排序是一种不稳定的排序算法。其时间复杂度和空间复杂度是：

Worst-case performance       O(N**2)Best-case  performance       O(N * logN)Average    performance       O(N * logN)Worst-case space complexity  O(N) auxiliary (naive)                             O(logN) auxiliary

参考资料：

1. https://interactivepython.org/courselib/static/pythonds/SortSearch/TheQuickSort.html
2. http://www.code2learn.com/2013/02/quick-sort-algorithm-tutorial.html
3. http://me.dt.in.th/page/Quicksort/

改进的快排序

在前面的讨论中，我们每次选取当前子表中的第一个对象作为基准对象(Pivot)。更好的选择是从第一个、中间一个与最后一个三者中选取关键字居中的对象作为基准。即pivot = median{Kl, K(l+r)/2, Kr}。 例如： median(10, 5, 7) = 7, median(10, 7, 7) = 7。

到此为止，我们已经弄明白了快排序。下一节，将介绍直接插入排序的改进版--希尔排序。